最近，2023考研最新大纲已陆陆续续的发布，大家在复习的同时要开始认真解读大纲，根据大纲来调整自己的复习计划。为了能够让忙碌中的考研学子们得到大纲变化，小编在这总结了相关内容，欢迎随时取阅。

2023考研数学(三)大纲变化之微积分

一、函数、极限、连续

【考试内容】

函数的概令及表示法函数的有界性，单调性，周期性和奇偶性 复合函数，反函数，分段函数和隐函数 基本初等函数的性质及其图形初等函数函数关系的建立

数列极限与函数极限的定义及其性质 函数的左极限和右极限无 穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则 两个重要极限;

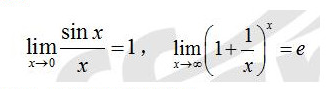
函数连续的概令 承数间断点的类型 初等承数的连续性 闭区间上连续承数的性质

【考试要求】

1.理解函数的概念，掌握函数的表示法，会建立应用问题的函数关系。

2.了解函数的有界性、单调性、周期性和奇偶性

3.理解复合函数及分段承数的概令，了解反承数及隐承数的概念，

4.堂握基本初等承数的性质及其图形，了解初等承数的概念，

5.理解极限的概念，理解函数左极限与右极限的概念以及函数极限存在与左极限，右极限之间的关系

6.了解极限的性质与极限存在的两个准则，堂握极限的四则运算法则，堂握利用两个重要极限求极限的方法。

7.理解无穷小量，无穷大量的概念，堂握无穷小量的比较方法，会用等价无穷小量求极限

8.理解函数连续性的概令(含左连续与右连续)，会判别承数间断点的类型

9.了解连续函数的性质和初等函数的连续性，理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理)，并会应用这些性质

二、一元函数微分学

【考试内容】

导数和微分的概念 导数的几何意义和经济意义 函数的可导性与连续性之间的关系 平面曲线的切线与法线 导数和微分的四则运算 基本初等函数的导数复合函数、反函数和隐函数的微分法高阶导数 一阶微分形式的不变性 微分中值定理 洛必达(L'Hospital)法则 函数单调性的判别 函数的极值 函数图形的凹凸性，拐点及渐近线承数图形的描绘承数的最大值与最小值

【考试要求】

1.理解导数的概念及可导性与连续性之间的关系，了解导数的几何意义与经济意义(含边际与弹性的概念)，会求平面曲线的切线方程和法线方程。

2.掌握基本初等函数的导数公式、导数的四则运算法则及复合函数的求导法则，会求分段函数的导数，会求反函数与隐函数的导数

3.了解高阶导数的概念，会求简单函数的高阶导数

4.了解微分的概念、导数与微分之间的关系以及一阶微分形式的不变性，会求函数的微分。

5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理，了解并会用柯西(Cauchy)中值定理

6.堂握用洛必达法则求夫定式极限的方法

7.掌握函数单调性的判别方法，了解函数极值的概念，掌握函数极值、最大值和最小值的求法及其应用

8.会用导数判断函数图形的凹凸性(注:在区间(a.b)内，设置函数f(x)有二阶导数，当f”(x)>0时，f(x)的图形是凹的，f”(x)<0,的图形是凸的)，会求函数图形的拐点以及水平、铅直和斜渐近线，会描绘函数的图形

三、一元函数积分学

【考试内容】

原函数和不定积分的概念 不定积分的基本性质 基本积分公式 定积分的概念和基本性质 定积分中值定理 积分上限的函数及其导数 牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法 反常(广义)积分定积分的应用

【考试要求】

1.理解原函数与不定积分的概念，掌握不定积分的基本性质和基本积分公式，掌握不定积分的换元积分法与分部积分法

2.了解定积分的概令和基本性质，了解定积分中值定理，理解积分上限的函数并会求它的导数，堂握牛顿-莱布尼茨公式以及定积分的换元积分法和分部积分法.

3.会利用定积分计算平面图形的面积、旋转体的体积和函数的平均值，会利用定积分求解简单的经济应用问题。

4.理解反常积分的概令，了解反常积分收敛的比较判别法，会计算反常积分

四、多元函数微积分学

【考试内容】

多元函数的概念 二元函数的几何意义 二元函数的极限与连续的概念 有界闭区域上二元连续函数的性质 多元函数偏导数的概念与计算 多元复合函数的求导法与隐函数求导法 二阶偏导数 全微分 多元函数的极值和条件极值，最大值和最小值 二重积分的念，基本性质和计算 无界区域上简单的反常二重积分

【考试要求】

1.了解多元函数的概念，了解二元函数的几何意义.

2.了解二元函数的极限与连续的概念，了解有界闭区域上二元连续函数的性质

3.了解多元函数偏导数与全微分的概念，会求多元复合函数一阶、二阶偏导数，会求全微分，了解隐函数存在定理，会求多元隐函数的偏导数

4.了解多元函数极值和条件极值的概念，掌握多元函数极值存在的必要条件，了解二元函数极值存在的充分条件，会求二元函数的极值，会用拉格朗日乘数法求条件极值，会求简单多元承数的最大值和最小值，并会解决一些简单的应用问题

5.理解二重积分的概令，了解一重积分的其本性质，了解二重和分的中信定理，堂握二重积分的计算方法(直角坐标、极坐标)，了解无思区域上较简单的反常二重积分并会计算.

五、无穷级数

【考试内容】

常数项级数的收敛与发散的概念 收敛级数的和的概念 级数的基本性质与收敛的必要条件 几何级数与p级数及其收敛性 正项级数收敛性的判别法 任意项级数的绝对收敛与条件收敛 交错级数与莱布尼茨定理 幂级数及其收敛半径、收敛区间(指开区间)和收敛域 幂级数的和函数 幕级数在其收敛区间内的基本性质，简单幂级数的和函数的求法，初等函数的暴级数展开式

【考试要求】

1.理解常数项级数收敛、发散以及收敛级数的和的概念，掌握级数的基本性质及收敛的必要条件。

2.堂握几何级数及p级数的收敛与发散的条件

3.掌握正项级数收敛性的比较判别法和比值判别法，根值判别法，会用积分判别法。

4.掌握交错级数的莱布尼茨判别法

5.了解任意项级数绝对收敛与条件收敛的概令以及绝对收敛与收敛的关系

6.理解幂级数收敛半径的概令，并掌握幂级数的收敛半径、收敛区间及收敛域的求法。

7.了解幕级数在其收敛区间内的基本性质(和函数的连续性、诼项求导和逐项积分)，会求一些暴级数在收敛区间内的和函数，并会由此求出某些数项级数的和.

8.掌握e，sinx，cosx，ln(1+x)及(1+x)“的麦克劳林(Maclaurin)展开式，会用它们将一下简单函数间接展开为幂级数。

六、常微分方程与差分方程

【考试内容】

常微分方程的基本概念 变量可分离的微分方程 齐次微分方程 一阶线性微分方程 线性微分方程解的性质及解的结构定理 二阶常系数齐次线性微分方程及简单的非齐次线性微分方程 差分与差分方程的概令 差分方程的通解与特解 一阶常系数线性差分方程 微分方程的简单应用

【考试要求】

1.了解微分方程及其阶、解、通解、初始条件和特解等概念

2.掌握变量可分离的微分方程、齐次微分方程和一阶线性微分方程的求解方法

3.理解线性微分方程解的性质及解的结构

4.堂握二阶常系数齐次线性微分方程的解法，并会解某些高干二阶的常系数齐次线性微分方程

5.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程

6.了解差分与差分方程及其通解与特解等概令

7.了解一阶常系数线性差分方程的求解方法

8.会用微分方程求解简单的经济应用问题

以上就是总结的“2023考研数学(三)大纲变化之微积分”全部内容，希望对大家有所帮助，更多的内容可关注湖南良师启航考研官网。