最近，2023考研最新大纲已陆陆续续的发布，大家在复习的同时要开始认真解读大纲，根据大纲来调整自己的复习计划。为了能够让忙碌中的考研学子们得到大纲变化，小编在这总结了相关内容，欢迎随时取阅。

2023考研数学(二)大纲变化之高等数学

一、函数、极限、连续

【考试内容】

函数的概念及表示法 函数的有界性、单调性、周期性和奇偶性 复合函数、反函数、分段函数和隐函数 基本初等函数的性质及其图形初等函数函数关系的建立 数列极限与函数极限的定义及其性质 函数的左极限与右极限 无穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则 两个重要极限:

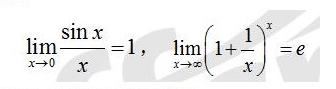
函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质

【考试要求】

1.理解函数的概念，掌握函数的表示法，并会建立应用问题的函数关系.

2.了解函数的有界性，单调性，周期性和奇偶性，

3.理解复合函数及分段函数的概念，了解反函数及隐函数的概念

4.堂握基本初等承数的性质及其图形，了解初等承数的概令，

5.理解极限的概念，理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.

6.掌握极限的性质及四则运算法则.

7.掌握极限存在的两个准则，并会利用它们求极限，掌握和用两个重要极限求极限的方法

8.理解无穷小量、无穷大量的概念，掌握无穷小量的比较方法，会用等价无穷小量求极限。

9.理解承数连续性的概令(含左连续与右连续)，会判别承数间断点的类型

10.了解连续函数的性质和初等函数的连续性，理解闭区间上连续函数的性质(有界性，最大值和最小值定理、介值定理)，并会应用这些性质

二、一元函数微分学

【考试内容】

导数和微分的概念 导数的几何意义和物理意义 函数的可导性与连续性之间的关系 平面曲线的切线和法线 导数和微分的四则运算 基本初等函数的导数 复合函数，反函数，隐函数以及参数方程所确定的函数的微分法 高阶导数一阶微分形式的不变性 微分中值定理 洛必达(L'Hospital)法则 函数单调性的判别 函数的极值 函数图形的凹凸性、拐点及渐近线，函数图形的描绘，函数的最大值与最小值 弧微分，曲率的概令，由率圆与曲率半径

【考试要求】

1.理解导数和微分的概令，理解导数与微分的关系，理解导数的儿但意义，会求平面曲线的切线方程和法线方程，了解导数的物理意义，会用导数描述一些物理量，理解函数的可导性与连续性之间的关系。

2.掌握导数的四则运算法则和复合函数的求导法则，掌握基本初等函数的导数公式。了解微分的四则运算法则和一阶微分形式的不变性，会求函数的微分

3.了解高阶导数的概念，会求简单函数的高阶导数

4.会求分段函数的导数，会求隐函数和由参数方程所确定的函数以及反函数的导数。

5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理，了解并会用柯西(Cauchy)中值定理

6.掌握用洛必达法则求未定式极限的方法。

7.理解函数的极值概念，掌握用导数判断函数的单调性和求函数极值的方法，掌握函数的最大值和最小值的求法及其应用

8.会用导数判断函数图形的凹凸性(注:在区间(a6)内，设函数f(x)具有二阶导数当f"(x)>0时，f(x)的图形是凹的;当f"(x)<0时，f(x)的图形是凸的)，会求函数图形的拐点以及水平、铅直和斜渐近线，会描绘函数的图形

9.了解曲率，曲率圆和曲率半径的概令，会计算曲率和曲率半径

三、一元函数积分学

【考试内容】

原承数和不定积分的概念，不定积分的基本性质 基本积分公式 定积分的概念和基本性质 定积分中值定理 积分上限的数其导数 牛顿-莱布尼茨(Newton-Leibniz)公式 不定积分和定积分的换元积分法与分部积分法 有理函数，三角函数有理式和简单无理函数的积分 反常(广义)积分 定积分的应用

【考试要求】

1.理解原函数的概念，理解不定积分和定积分的概念

2.堂握不定和分的其本公式，掌握不定和分和定和分的性质及定和分中借定理，常握换元和分法与分部和分法

3.会求有理函数、三角函数有理式和简单无理函数的积分

4.理解积分上限的承数，会求它的导数，堂握牛顿-莱布尼茨公式

5.了解反常积分的概念，了解反常积分收敛的比较判别法，会计算反常积分

6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值。

四、多元函数微积分学

【考试内容】

多元函数的概念一二元函数的几何意义 二元函数的极限与连续的概念 有界闭区域上二元连续函数的性质 多元函数的偏导数和全微分多元复合函数。

隐函数的求导法 二阶偏导数 多元函数的极值和条件极值、最大值和最小值，二重积分的概念、基本性质和计算

【考试要求】

1.了解多元函数的概令，了解二元函数的几何意义

2.了解二元函数的极限与连续的概念，了解有界闭区域上二元连续函数的性质

3.了解多元函数偏导数与全微分的相令，会求多元复合函数一阶，一阶偏导数，会求全微分，了解隐承数存在定理，会求多元隐函数的偏导数

4.了解多元函数极值和条件极值的概念，掌握多元函数极值存在的必要条件，了解二元函数极值存在的充分条件，会求二元函数的极值，会用拉格朗日乘

数法求条件极值，会求简单多元函数的最大值和最小值，并会解决一些简单的应用问题

5.理解二重积分的概念，了解二重积分的基本性质，了解二重积分的中值定理，堂握二重积分的计算方法(直角坐标，极坐标)。

五、常微分方程

【考试内容】

常微分方程的其本概念 变量可分离的微分方程 齐次微分方程一阶线性微分方程 可降阶的高阶微分方程 线性微分方程解的性质及解的结构定理 二阶常系数齐次线性微分方程 高于二阶的某些常系数齐次线性微分方程 简单的二阶常系数非齐次线性微分方程微分方程的简单应用

【考试要求】

1.了解微分方程及其阶，解，通解，初始条件和特解等概令

2.堂握变量可分离的微分方程及一阶线性微分方程的解法，会解齐次微分方程，

3.会用降阶法解下列形式的微分方程:y(n)=f(x)，y"=f(x，y)和y"=f(y，y").

4.理解线性微分方程解的性质及解的结构

5.堂握二阶常系数齐次线性微分方程的解法，并会解某些高干二阶的常系数齐次线性微分方程

6.会解自由项为多项式，指数承数，正弦函数，余弦函数以及它们的和与和的一阶堂系数非齐次线性微分方程

7.会用微分方程解决一些简单的应用问题

以上就是总结的“2023考研数学(二)大纲变化之高等数学”全部内容，希望对大家有所帮助，更多的内容可关注湖南良师启航考研官网。